Overview of GridPACK
Bruce Palmer, William Perkins, Kevin Glass, Yousu Chen, Shuangshuang Jin, David Callahan, Ruisheng Diao, Mark Rice, Stephen Elbert, Zhenyu Huang
Introduction
The objective of the GridPACK™ toolkit project is to develop a framework to support the rapid development of power grid applications capable of running on high performance computing architectures (HPC) with high levels of performance and scalability. The toolkit will allow power system engineers to focus on developing working applications from their models without getting bogged down in the details of decomposing the computation across multiple processors, managing data transfers between processors, working out index transformations between power grid networks and the matrices generated by different power applications, and managing input and output. GridPACK™ is being designed to encapsulate as much of the book-keeping required to set up HPC applications as possible in high-level programming abstractions that allow developers to concentrate on the physics and mathematics of their problems.
This report will summarize the overall design of the GridPACK™ framework. The initial focus of the GridPACK™ design analysis was to target four power grid applications and to identify common features that span multiple applications as candidates for inclusion in a framework. This analysis included a breakdown of the application into phases and identification within each phase of the functionality required to complete them. The four applications originally targeted within this project were power flow simulations, contingency analysis, state estimation and dynamic simulation. The remainder of this document will describe the effort to obtain design requirements to determine what functionality the GridPACK™ framework would need to incorporate in order to support multiple power grid applications and the initial framework design that resulted from these requirements. The framework will continue to evolve as more real-world experience can be incorporated into the design process but many base classes that have already been identified that are capable of supporting a range of applications.
Four power grid applications were targeted for initial implementation within the GridPack framework. These consisted of
- Powerflow simulations of the electric grid
- Contingency analysis of the electric grid
- State estimation based on electric grid measurements
- Dynamic simulations of the electric grid
Based on these applications, several cross-cutting functionalities were identified that could be used to support multiple applications. These include modules to support
- Network topology and behavior. The network topology is the starting point for any power grid analysis. The topology defines the initial network model and is the connection point between the physical problem definition in terms of buses and branches and the solution method, which is usually expressed in terms of matrices and vectors.
- Network components and their properties (e.g. bus and branch models, measurements, etc.) grid components are the objects associated with the buses and branches of the power grid network. Along with the network topology itself, these define the physical system being modeled and in some cases the analysis that is to be performed. Bus and branch components can be differentiated into things like generators, loads, grounds, lines, transformers, measurements, etc. and depending on the how they are defined and the level of detail incorporated into them, they define different power grid systems and analyses. The behavior of buses and branches can depend on the properties of branches or buses that are directly attached to them, e.g. figuring out the contribution of a particular bus to the solution procedure may require that properties of the branches attached to that bus are made available to the bus. The necessity for exchanging this data is built into the framework. Furthermore, these data exchanges must also be accounted for in a parallel computing context, since the grid component from which data is required may be located on a different processor.
- Linear algebra and solvers. Basic algebraic objects, such as distributed matrices and vectors, are a core part of the solution algorithms required by power grid analyses. Most solution algorithms are dominated by sparse matrices but a few, such as Kalman filter analyses, require dense matrices. Vectors are typically dense. There exists a rich set of libraries for constructing distributed matrices and vectors and these are coupled to preconditioner and solver libraries. GridPACK™ can leverage this work heavily by creating wrappers within the framework to create matrices and vectors that can be used in solution algorithms. Wrapping these libraries instead of using them directly will have the advantage that creating these algebraic objects can be simplified somewhat for power grid applications but more importantly, it will allow framework developers to investigate new solver and algebraic libraries seamlessly, without disrupting other parts of the code.
- Mapping between network and algebraic objects. The physical properties of power grid systems are defined by networks and the properties of the network components but the equations describing the networks are algebraic in nature. The mappings between the physical networks and the algebraic equations depend on the indexing scheme used to describe the network and the number of parameters in the network components that appear in the equations. Constructing a map between network parameters and their corresponding locations in a matrix or vector can be complicated and error prone. Fortunately, much of this work can be automated and developers can focus much more on developing code to evaluate individual matrix elements without worrying about where to locate them in the matrix. This can considerably simplify coding.
GridPACK™ Framework Components
This section will describe the core components identified so far and the functionality they support. It will start off with two components that directly support the major underlying data objects, the power grid network and its associated network components and matrices and vectors. Additional components are then built on top of these (or at least in conjunction with them). These include partitioners to sort out the grid among the processors, grid components that describe the physics of the different network models or analyses, grid component factories that initialize the grid components, mappers that convert the current state of the grid components into matrices and vectors that are used in the solution algorithms, solvers that supply the preconditioner and solver functionality necessary to implement solution algorithms, input and output modules that allow developers to import and export data, and other utility modules that support standard code develop operations like timing, event logging, and error handling.
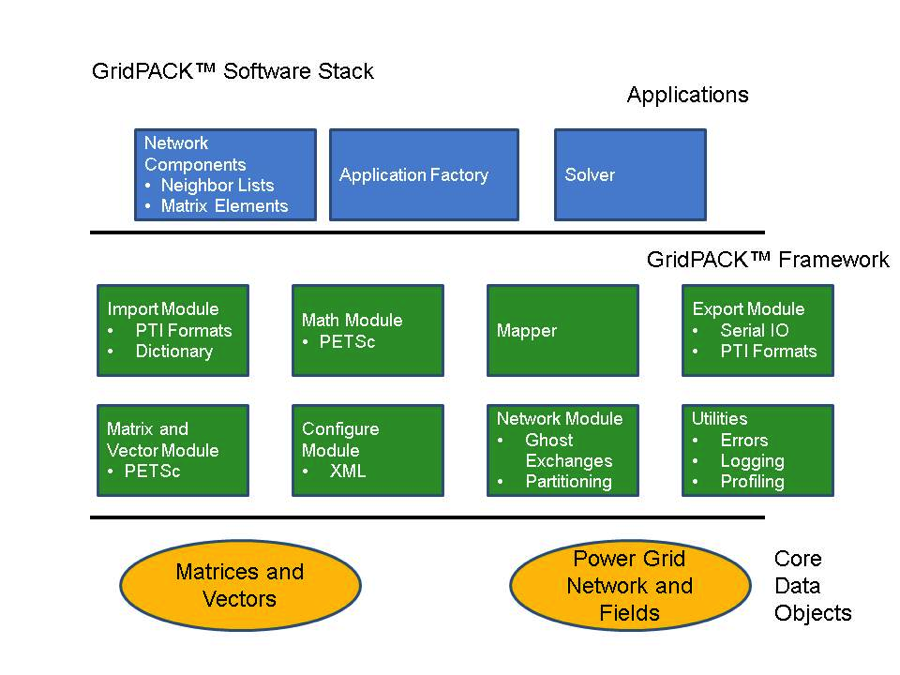
Many of these modules are constructed using libraries developed elsewhere so as to minimize framework development time. However, by wrapping these libraries in interfaces geared towards power grid applications these libraries can be made easier to use by power grid engineers. The interfaces also make it possible to exchange libraries in the future for new or improved implementations of specific functionality without requiring application developers to rewrite their codes. This can significantly reduce the cost of introducing new technology into the framework. The software layers in the GridPACK™ framework are shown schematically in Figure 1.
Figure 1. A schematic diagram of the GridPack framework software data stack. PETSc is an external library that supports distributed matrices and vectors and supplies extensive support for parallel algebraic operations and linear and non-linear solvers.
Core framework components are described below. Before discussing the components themselves, some of the coding conventions and libraries used in GridPACK™ will be described.
Preliminaries: The GridPACK™ software uses a few coding conventions to help improve memory management and to minimize run-time errors. The first of these is to employ namespaces for all GridPACK modules. The entire GridPACK™ framework uses the gridpack namespace, individual modules within GridPACK™ are further delimited by their own namespaces. For example, the BaseNetwork class discussed in the next section resides in the gridpack::network namespace and other modules have similar delineations. The example applications included in the source code also have their own namespaces, but this is not a requirement for developing GridPACK™-based applications.
To help with memory management, many GridPACK™ functions return boost shared pointers instead of conventional C++ pointers. These can be converted to a conventional pointer using the get() command. We also recommend that pointers be converted using a dynamic_cast instead of conventional C-style cast.
Network Module: the network module is designed as a container with four major functions
- The network is a container for the network topology. The connectivity of the network is maintained by the network object and can be made available through requests to the network. The network also maintains the “ghost” status of locally held buses and branches and determines whether a bus or branch is owned by a particular processor or represents a ghost image of a bus or branch owned by a neighboring processor.
- The network topology can then be decorated with bus and branch objects that reflect the properties of the particular physical system under investigation. These bus and branch objects are written by the application developer and reflect the particular physical system under investigation and the analyses that need to be performed on it. Different applications will use different bus and branch implementations.
- The network module is responsible for implementing update operations that can be used to fill in the value of ghost cell fields with current data from other processors. The update of ghost buses and ghost branches have been split into separate operations to give users flexibility in optimizing performance by minimizing the amount of data that needs to be communicated in the code.
- The network contains the partitioner. The partitioner is embedded in the network module but represents a substantial technology in its own right. Partitioning is a key part of parallel application development. It represents the act of dividing up the problem so that each processor is left with approximately equal amounts of work and so that communication between processors (a major source of computational inefficiency in HPC programs) is minimized.
A major use of the partitioner is to rearrange the network in a form that is useful for computation immediately after it is read in from an external file. Typically, the information in the external file is not organized in a way that is necessarily useful for computation, so the partitioner must reorganize data such that large connected blocks are all on the same processor. The partitioner is also responsible for adding the ghost buses and branches to the system.
Ghost buses and branches in a parallel program represent images of buses and branches that are owned by other processes. In order to carry out operations on buses and branches it is frequently necessary to gain access to data associated with attached buses and branches. The most efficient way to do this is to create copies of the buses and branches from other processors on each process so that all locally own objects are attached to these copies (ghosts). The ghost objects are then updated collectively with current information from their home processors at points in the computation. Updating all ghosts at once is almost always more efficient than access data from one bus or branch at a time.
A major use of the partitioner is to rearrange the network in a form that is useful for computation immediately after it is read in from an external file. Typically, the information in the external file is not organized in a way that is necessarily useful for computation, so the partitioner must reorganize data such that large connected blocks are all on the same processor. The partitioner is also responsible for adding the ghost buses and branches to the system.
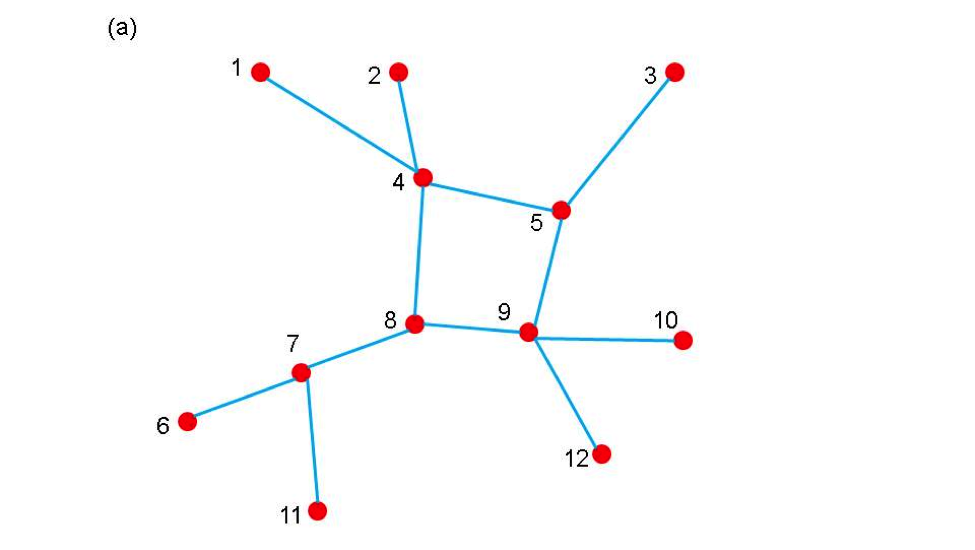
Ghost buses and branches in a parallel program represent images of buses and branches that are owned by other processes. In order to carry out operations on buses and branches it is frequently necessary to gain access to data associated with attached buses and branches. The most efficient way to do this is to create copies of the buses and branches from other processors on each process so that all locally own objects are attached to these copies (ghosts). The ghost objects are then updated collectively with current information from their home processors at points in the computation. Updating all ghosts at once is almost always more efficient than access data from one bus or branch at a time. The use of the partitioner to distribute the network between different processors and create ghost nodes and branches is illustrated in Figure 2. Figure 2(a) shows a simple network and Figures 2(b) and 2(c) show the result of distributing the network between two processors.
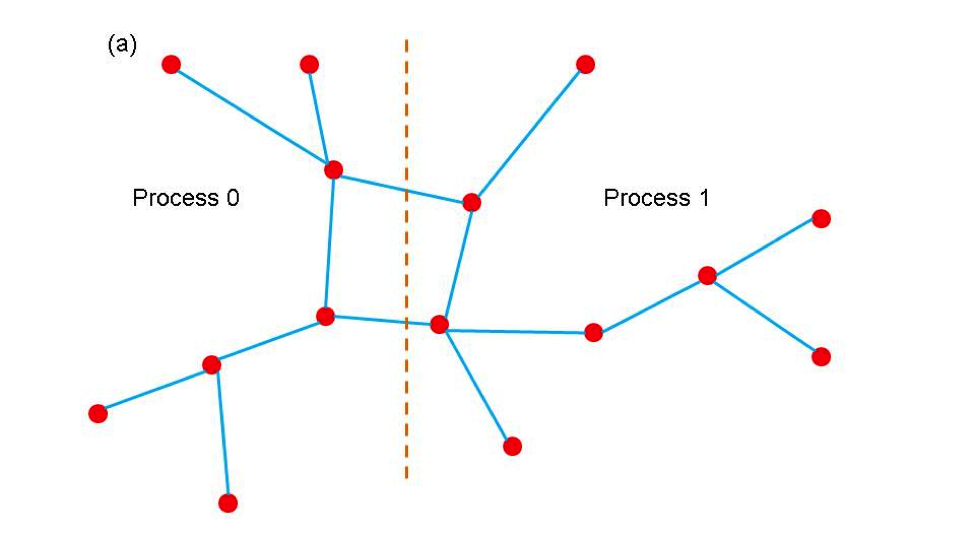
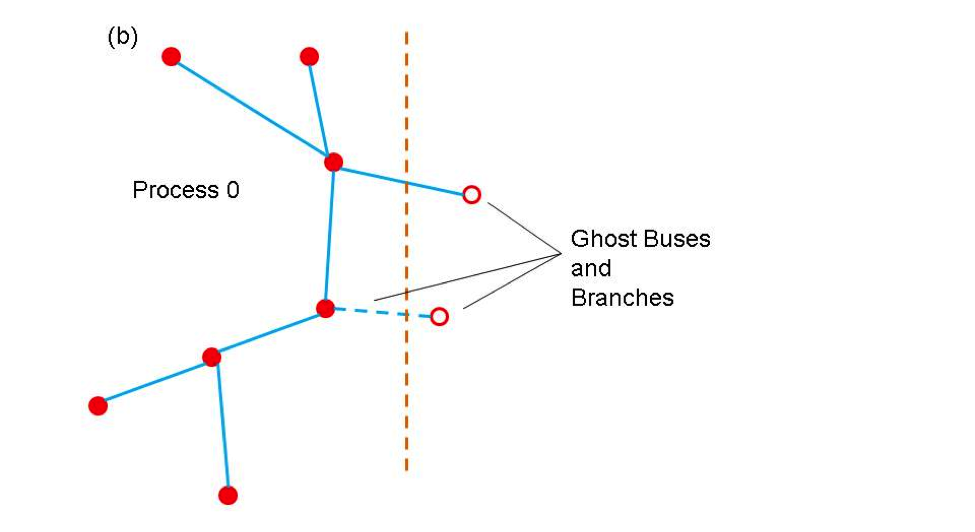
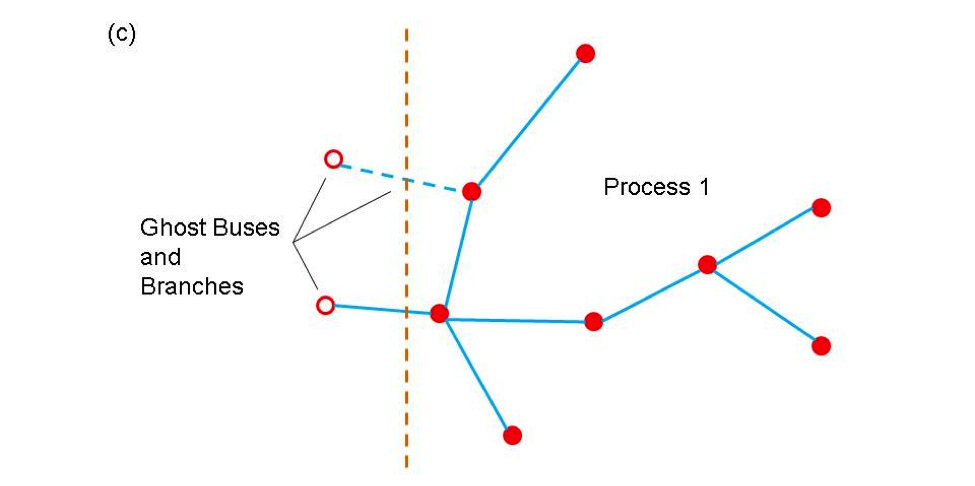 Figure 2. (a) a simple network (b) partition of network on processor 0 (c) partition of network on processor 1. Open circles indicate ghost buses and dotted lines indicate ghost branches.
Figure 2. (a) a simple network (b) partition of network on processor 0 (c) partition of network on processor 1. Open circles indicate ghost buses and dotted lines indicate ghost branches.
Networks can be created using the templated base class BaseNetwork<class Bus, class Branch>, where Bus and Branch are application specific classes describing the properties of buses and branches in the network. The BaseNetwork class is defined within the gridpack::network namespace and uses the header file gridpack/network/base_network.hpp. In addition to the Bus and Branch classes, each bus and branch has an associated DataCollection object, which is described in more detail in the network components section. The DataCollection object is a collection of key-value pairs that acts as an intermediary between data that is read in from external configuration files and the bus and branch classes that define the network.
The BaseNetwork class contains a large number of methods, but only a relatively small number will be of interest to application developers. Most of the remaining methods are used primarily within other GridPACK™ modules to implement higher level capabilities. This document will focus on calls that are likely to be used by application developers.
The constructor for the network class is the function
BaseNetwork(const parallel::Communicator &comm)
The Communicator object can be used to define the set of processors over which the network is distributed. This constructor creates an empty shell does not contain any information about an actual network. The remainder of the network must be built up by adding buses and branches to it. Typically, buses and branches are added by passing the network to a parser (see import module) which will create an initial version of the network. The constructor is paired with a corresponding destructor
~BaseNetwork()
that is called when the network object passes out of scope or is explicitly deleted by the user.
Two functions are available that return the number of buses or branches that are available locally on a process. This number includes both locally held buses and branches as well as any ghosts that may be located on the process.
int numBuses() int numBranches()
There are also functions that will return the total number of buses or branches in the network. These numbers ignore ghosts buses and ghost branches.
int totalBuses() int totalBranches()
Buses and branches in the network can be identified using a local index that runs from 0 to one minus that number of buses or branches on the process (0-based indexing). For some calculations, it is necessary to identify one bus in the network as a reference bus. This bus is usually set when the network is created using an import parser. It can subsequently be identified using the function
int getReferenceBus()
If the reference bus is located on this processor (either as a local bus or a ghost) then this function returns the local index of the bus, otherwise it returns -1.
Ghost buses and branches are distinguished from locally owned buses and branches based on whether or not they are “active”. The two functions
bool getActiveBus(int idx) bool getActiveBranch(int idx)
provide the active status of a bus or branch on a process. The index idx is a local index for the bus or branch.
Buses and branches are characterized by a number of different indices. One is the local index, already discussed above, but there are several others. Most of these are used internally by other parts of the framework but on index is of interest to application developers. This is the “original” bus index. When the network is described in the input file, the buses are labeled with a (usually) positive integer. There or no requirements that this integer be consecutive, only that each bus has its own unique index. The value of this index can be recovered using the function
int getOriginalBusIndex(int idx)
The variable idx is the local index of the bus. Branches are usually described in terms of the original bus indices for the two buses at each end of the branch, so there is no corresponding function for branches. Instead, the procedure is to get the local indices of the two buses at each end of the branch and then get the corresponding original indices of the buses. This information is usually used for output.
It is frequently necessary to gain access to the objects associated with each bus or branch. The following four methods can be used to access these objects
boost::shared_ptr<Bus> getBus(int idx) boost::shared_ptr<Branch> getBranch(int idx) boost::shared_ptr<DataCollection> getBusData(int idx) boost::shared_ptr<DataCollection> getBranchData(int idx)
The first two methods can be used to get Boost shared pointers to individual bus or branch objects indexed by local indices idx. The second two functions return pointers to the DataCollection objects associated with each bus or branch. These objects are usually used to initialize the bus and branch objects at the start of a calculation
void partition()
The partition function distributes the buses and branches across processers such the connectivity to branches and buses on other processors is minimized. It is also responsible for adding the ghost buses and branches to the network. This function should be called after the network is read in but before any other operations, such as setting up exchange buffers or creating neighbor lists have been performed.
Finally, two sets of functions are required in order to set up and execute data exchanges between buses and branches in a distributed network. These exchanges are used to move data from active components to ghost components residing on other processors. Before these functions can be called, the buffers in individual network components must be allocated. See the documentation below on network components and the network factory for more information on how to do this. Once the buffers are in place, bus and branch exchanges can be set up and executed with just a few calls. The functions
void initBusUpdate() void initBranchUpdate()
are used to initialize the data structures inside the network object that manage data exchanges. Exchanges between buses and branches are handled separately, since not all applications will require exchanges between both sets of objects. The initialization routines are relatively complex and allocate several large internal data structures so they should not be called if there is no need to exchange data between buses or branches.
After the updates have been initialized, it is possible to execute a data exchange at any point in the code by calling the functions
void updateBuses() void updateBranches()
These functions will actually cause data to be exchanged between active buses and branches and their corresponding ghosts buses and branches located on other processors.
The BaseNetwork methods described above are only a subset of the total functionality available but they represent most of the functionality that a typical developer would use. The remaining functions are primarily used to implement other parts of the GridPACK™ framework but are generally not required by people writing applications.
Math Module:the math module is used to provide support for distributed matrices and vectors as well as linear solvers, non-linear solvers, and preconditioners. Once created, matrices can be treated as opaque objects and manipulated using a high level syntax that would comparable to writing Matlab code. The distributed matrix and vector data structures themselves are based on existing solver libraries and represent relatively lightweight wrappers on existing code. The current math module is built on the PETSc library but other libraries, such as Hypre and Trilinos could be used instead to implement the math module.
The main functionality associated with the math module is the ability to instantiate new matrices and vectors, add individual matrix and vector elements (and their values) to the matrix/vector objects and invoke and assemble operation on the object. The assemble operation is designed to give the library a chance to set up internal data structures and repartition the matrix elements, etc. in a way that will optimize subsequent calculations. Inclusion of this operation also follows the syntax of most solver libraries when they construct a matrix or vector. This module also includes some basic matrix and vector operations such as matrix-vector multiply and norms.
In addition to basic matrix operations, the math module contains linear and non-linear solvers and preconditioners. The math module provided a simple interface on top of the PETSc libraries that will allow users access to this functionality without having to be familiar with the libraries themselves. This should make it possible to construct solver routines that are comparable in complexity to Matlab scripts. The use of a wrapper instead of having users directly access the libraries will also make it simpler to switch the underlying library in an application. All that will be required will be for developers to link to a different implementation of the math module interface that is built on a different library. There will not be any need to rewrite any application code. This has the advantage that if a different library is used for the math module in one application, it instantly becomes available for other applications.
The functionality in the math component is distributed between for classes, Matrix, Vector, LinearSolver and NonlinearSolver<code>. Each of the classes is in the <code>gridpack::math namespace and is described below. These classes use the gridpack/math/matrix.hpp, gridpack/math/vector.hpp, gridpack/math/linear_solver.hpp and gridpack/math/nonlinear_solver.hpp header files. Like the BaseNetwork class, there are a lot of functions in Matrix and Vector that do not need to be used by users. Most of the functions related to matrix/vector instantiation and creation are actually located inside the mapper classes described below.
The Matrix class is designed to create distributed matrices. It supports two types of matrix, Dense and Sparse. In most cases users will want to use the sparse matrix but some applications require dense matrices. The matrix constructor is
Matrix(const parallel::Communicator &dist,
const int &local_rows,
const int &cols,
const StorageType &storage_type=Sparse)
The communicator object dist specifies the set of processors that the matrix is defined on, the local_rows parameter corresponds to the number of rows contributed to the matrix by the processor, the cols parameter indicates what the second dimension of the matrix is and the storage_type parameter determines whether the matrix is sparse or dense. If the total dimension of the matrix is M×N, then the sum of the local_rows parameters over all processors must equal M and the cols parameter is equal to N. The matrix destructor is
~Matrix()
Once a matrix has been created some inquiry functions can be used to probe the matrix size and distribution. The following functions return information about the matrix.
int rows() const int localRows() const void localRowRange(int &lo, int &hi) const int cols()
The function rows will return the total number of rows in the matrix, localRows returns the number of rows associated with the calling processor, localRowRange returns the lo and hi index of the rows associated with the calling processor and cols returns the number of columns in the matrix. Note that matrices are partitioned into row blocks on each processor.
Addition functions can be used to add matrix elements to the matrix, either one at a time or in blocks. The following two calls can be used to reset existing elements or insert new ones.
void setElement(const int &i, const int &j,
const ComplexType &x)
void setElements(const int &n, const int *i, const int *j,
const ComplexType *x)
The first function will set the matrix element at the index location <code>(i,j) to the value x. If the matrix element already exists, this function overwrites the value, if the element is not already part of the matrix, it gets added with the value x. Note that both i and j are zero-based indices. For the current PETSc based implementation of the math module, it is not required that the index i lie between the values of lo and hi obtained with localRowRange function, but for performance reasons it is desirable. Other implementations may require that i lie in this range. The second function can be used to add a collection of elements all at once. This can result in improved performance. The variable n is the number elements to be added, the arrays i and j contain the row and column indices of the matrix elements and the array x contains their values. Again, it is preferable that all values in i lie within the range [lo,hi].
Two functions that are similar to the set element functions above are the functions
void addElement(const int &i, const int &j,
const ComplexType &x)
void addElements(const int &n, const int *i, const int *j,
const ComplexType *x)
These differ from the set element functions only in that instead of overwriting or inserting the new values into the matrix, these functions will add the new values to whatever is already there. If no value is present in the matrix at that location the function inserts it.
In addition to setting or adding new elements, it is possible to retrieve matrix values using the functions
void getElement(const int &i, const int &j,
ComplexType &x) const
void getElements(const int &n, const int *i, const int *j,
ComplexType *x) const
These functions can only access elements that are local to the processor. This means that the index i must lie in the range [lo,hi] returned by the function localRowRange.
Finally, before a matrix can be used in computations, it must be assembled and internal data structures must be set up. This can be accomplished by calling the function
void ready()
After this function has been invoked, the matrix is read for use and can be used in computations. In general, the procedure for building a matrix is 1) create the matrix object 2) determine local parameters such as lo and hi 3) set or add matrix elements and 4) assemble matrix using the ready function. Note that users can often avoid most of these operations by building matrices and vectors using the mapper functionality described below.
Some additional functions have been included in the matrix class that can be useful for creating matrices or writing out their values (e.g. for debugging purposes). It is often useful to create a copy of a matrix. This can be done using the clone method
Matrix* clone() const
The new matrix is an exact replica of the matrix that invokes this function.
Two functions that can be used to write the contents of a matrix, either to standard output or to a file are
void print (const char *filename=NULL) const void save(const char *filename) const
The first function will write the contents of the matrix to standard output if no filename is specified, otherwise it writes to the specified file, the second function will write a file in MatLAB format. These functions can be used for debugging or to create matrices that can be fed into other programs.
Once a matrix has been created, a variety of methods can be applied to it. Most of these are applied after the ready call has been made by the matrix, but some operations can be used to actually build a matrix. These functions are listed below.
void equate(const Matrix &A)
This function sets the calling matrix equal to matrix A. This assumes that the calling matrix has been created but no matrix elements have been added to it.
void scale(const ComplexType &x)
Multiply all matrix elements by the value x.
void multiplyDiagonal(const Vector &x)
Multiply all elements on the diagonal of the calling matrix by the vector x. The Vector class is described below.
void add(const Matrix &A)
Add the matrix A to the calling matrix. The two matrices must have the same number of rows and columns, but otherwise there are no restrictions on the data layout or the number and location of the non-zero entries.
void identity()
Create an identity matrix. This function assumes that the calling matrix has been created but no matrix elements have been assigned to it.
void zero()
Set all non-zero entries to zero.
The math module also contains solvers. The LinearSolver class contains a constructor
LinearSolver(const Matrix &A)
that creates an instance of the solver. The matrix A defines the set of linear equations Ax=b that must be solved. The properties of the solver can be modified by calling the function
void configure(utility::Configuration::Cursor *props)
The Configuration module is described in more detail below. This function can be used to pass information from the input file to the solver to alter its properties.
Finally, the solver can be used to solve the set of linear equations by calling the method
void solve(const Vector &b, Vector &x) const
This function returns the solution x based on the right hand side vector b.
Network Components: Network component is a generic term for objects associated with buses and branches. These objects determine the behavior of the system and the type of analyses being done. Branch components can represent transmission lines and transformers while bus components could model loads, generators, or something else. Both kinds of components could represent measurements (e.g. for a state estimation analysis).
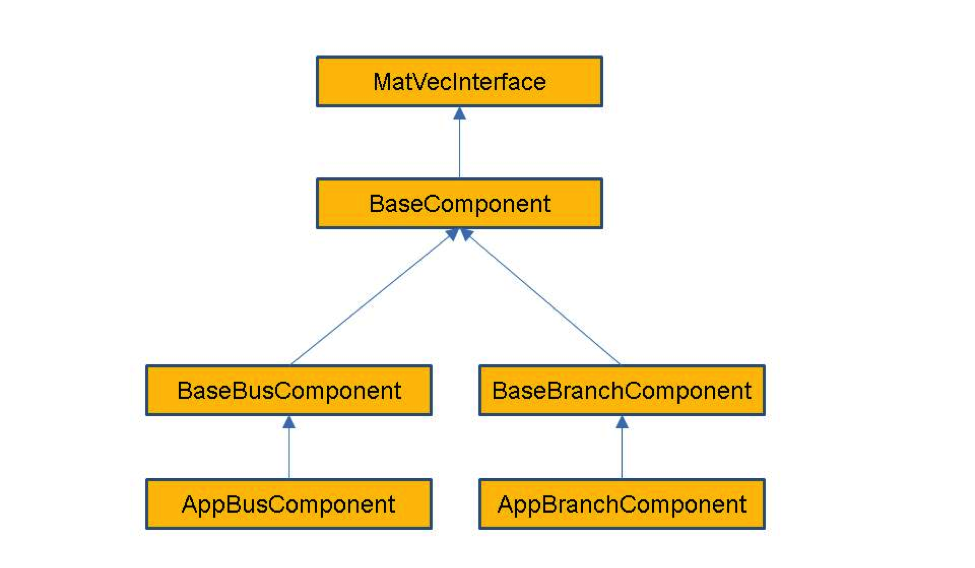
Network components cover a fairly broad range of behaviors and there is little that can be said about them outside the context of a specific problem. Each component inherits from a matrix-vector interface, which enables the framework to generate matrices and vectors from the network in a relatively straightforward way. In addition, buses inherit from a base bus interface and branches inherit from a base branch interface. The relationship between these interfaces is shown if Figure 3.
Figure 3. Schematic diagram showing the interface hierarchy for network components.
These base interfaces provide mechanisms for accessing the neighbors of a bus or branch and allow developers to specify what data is transferred in ghost exchanges. They do not define any physical properties of the bus or branch, it is up to application developers to do this.
Of these interfaces, the matrix-vector interface is the most important. It answers the question what block of data is contributed by a bus or network and what the dimensions of the block are. For example, if constructing the Y-matrix for a power flow problem using a real-valued formulation, the grid components on buses contribute a 2×2 block to the diagonal of the matrix. Similarly, the grid components on branches contribute a 2×2 block to the off-diagonal elements. (Note that if the Y-matrix is expressed as a complex matrix, then the blocks are of size 1×1.) The location of these blocks in the matrix is determined by the location of the corresponding buses and branches in the network, but the indexing calculations required to determine this location can be made completely transparent to the user via the mapper module.
Because the matrix-vector interface focuses on small blocks, it should be relatively easy for power grid engineers to write the corresponding methods. The full matrices and vectors can then be generated from the network using relatively simple calls to the mapper interface (see the discussion below on the mapper module). All of the base network component classes reside in the gridpack::component namespace and use the gridpack/component/base_component.hpp header file.
The MatVecInterface is probably the most important of the network component base classes, it is also the most difficult to understand. Its primary function is to enable developers to build the matrices and vectors used in the solution algorithms from the network. It eliminates a large amount of tedious and error-prone index calculations that would otherwise need to performed in order to determine where in a matrix a particular data element should be placed. The MatVecInterface includes basic constructors and destructors. The first set of non-trivial operations are generally implemented on buses and set the values of diagonal blocks in the matrix. Additional functions are usually implemented on branches and set values for off-diagonal elements. Vectors can be created by calling functions from buses. These functions are described in detail below.
The two functions that are used to create diagonal matrix blocks are
virtual bool matrixDiagSize(int *isize, int *jsize) const virtual bool matrixDiagValues(ComplexType *values)
Both functions are virtual functions and are expected to be overwritten by application specific bus and branch classes. The default behavior is to return 0 for isize and jsize and to return false for both functions. This means that these functions will not build a matrix unless overwritten by the application. Not all functions need to be overwritten by a given bus or branch class. Generally, only a subset of functions may be needed by an application.
The matrixDiagSize function returns the size of the matrix block that is contributed by the bus to a matrix. If a single complex number is contributed by the bus, the matrixDiagSize function returns 1 for both isize and jsize. If a real-valued formulation is being used so that the single returned values is expressed as a 2×2 block then both isize and jsize are set to 2. The return value is true if the bus contributes to the matrix, otherwise it is false. This can occur, for example, if the bus is the reference bus in power flow calculation. For a more complicated calculation, such as a dynamic simulation with multiple generators on some buses, the size of the matrix blocks can differ from bus to bus. Note that the values returned by matrixDiagSize refer only to the particular bus that is invoking the function. It does not say anything about other buses in the system.
The matrixDiagValues function returns the actual values for the matrix block associated with the bus for which the function is invoked. The values are returned as a linear array with values returned in row-major order. For a 2×2 block, this means the first value is at the (0,0) position, the second value is at the (1,0) position, the third values is at the (0,1) position and the fourth value is at the (0,0) position. This function also returns true if the bus contributes to the matrix and false otherwise. This may seem redundant, since the matrixDiagSize function has already returned this information but it turns out there are certain applications where it is desirable for the matrixDiagSize function to return true and the matrixDiagValues function to return false. The buffer values is supplied by the calling program and is expected to be big enough, based on the dimensions returned by the matrixDiagSize function, to contain all returned values.
The functions that are used to return values for off-diagonal matrix elements are listed below. These are usually only implemented for branches.
virtual bool matrixForwardSize(int *isize, int *jsize) const virtual bool matrixForwardValues(ComplexType *values) virtual bool matrixReverseSize(int *isize, int *jsize) const virtual bool matrixReverseValues(ComplexType *values)
These functions work in a similar way to the functions for creating blocks along the diagonal, except that the split off-diagonal matrix calculations into forward elements and reverse elements. The initial approximate location of an off-diagonal matrix element in a matrix is based in some internal indices assigned to the buses at either end of the branch. Suppose that these indices are i, corresponding to the “from” bus and j, corresponding to the “to” bus. The “forward” functions assume that the request is for the ij element while the “reverse” functions assume that the request is for the ji element. Another way of looking at this is the following: as discussed below, branches contain pointers to two buses. The first is the “from” bus and the second is the “to” bus. The forward functions assume that the “from” bus corresponds to the first index of the element, the reverse functions assume that the “from” bus corresponds to the second index of the element. Note that if a bus does not contribute to a matrix, then the branches that are connected to the bus should also not contribute to the matrix.
The final set of functions in the MatVecInterface that are of interest to application developers are designed to set up vectors. These are usually implemented only for buses. The following two functions are analogous to the functions for creating matrix elements
virtual bool vectorSize(int *isize) const virtual bool vectorValues(ComplexType *values)
The vectorSize function returns the number of elements contributed to the vector by a bus and the vectorValues returns the corresponding values. The vectorValues function expects the buffer values to be allocated by the calling program. In addition to functions that can be used to specify a vector, there is an additional function that can be used to push values from a vector back onto a bus. This function is
virtual void setValues(ComplexType *values)
The buffer contains values from the vector corresponding to internal variables in the bus and this function can be used to set the bus variables. The setValues function could be used to assign bus variables so that they can be used to recalculate matrices and vectors for an iterative loop in a non-linear solver or so that the results of a calculation can be exported to an output file.
The BaseComponent class contains additional functions that contribute to the base properties of a bus or branch. Again, most of the functions in this class are virtual and are expected to be overwritten by actual implementations. However, not all of them need to be overwritten by a particular bus or branch class. Many of these functions are used in conjunction with the BaseFactory class, which defines methods that run over all buses and branches in the network and invokes the functions defined below.
The load function
virtual void load(const boost::shared_ptr<DataCollection> &data)
is used to instantiate components based on data that is located in the network configuration file that is used to create the network. It is used in conjunction with the DataCollection object, which is described in more detail below. Networks are generally created by first instantiating a network parser and then using this to read in an external network file and create the network topology. The next step is to invoke the partition function on the network to get all network element properly distributed between processors. At this point, the network, including ghost buses and branches, is complete and each bus and branch has a DataCollection object containing all the data in the network configuration file that pertains to that particular bus or branch. The data in the DataCollection object is stored as simple key-value pairs. The next step is to use the data to instantiate the in the DataCollection object initialize the corresponding bus or branch. This occurs when the load function is invoked on all buses and branches in the system. The bus and branch classes must implement this function to extract the correct parameters from the DataCollection object and use them to assign internal bus and branch parameters.
Only one type of bus and one type of branch is associated with each network but many different types of equations can be generated by the network. To allow developers to embed many different behaviors into a single network and to control at what points in the simulation those behaviors can be manifested, the concept of modes is used. The function
virtual void setMode(int mode)
can be used to set an internal variable in the component that tells it how to behave. The variable “mode” usually corresponds to an enumerated constant that is part of the application definition. For example, in a power flow calculation it might be necessary to calculate both the Y-matrix and the equations for the power flow solution containing the Jacobian matrix and the right-hand side vector. To control which matrix gets created, two modes are defined: “YBus” and “Jacobian”. Inside the matrix functions in the MatVecInterface, there is a condition
if (p_mode == YBus) {
// Return values for Y-matrix calculation
} else if (p_mode == Jacobian) {
// Return values for power flow calculation
}
The variable “p_mode” is an internal variable in the bus or branch that is set using the setMode function.
The function
virtual bool serialWrite(char *string, const char *signal = NULL)
is used in the serial IO modules described below to write out properties of buses or branches to standard output. The character buffer “string” contains a formatted line of text representing the properties of the bus or branch that is written to standard output, the variable “signal” can be used to control what data is written out and the return value is true if the bus or branch is writing out data and false otherwise. For example, if the application is writing out the properties of all buses with generators, then the signal “generator” might be passed to this subroutine. If a bus has generators, then a string is copied into the buffer “string” and the function returns true, otherwise it returns false. The buffer “string” is allocated by the calling program.
The BaseComponent class also contains two functions that must be implemented if buses and/or branches need to exchange data with other processors. Data that must be exchanged needs to be placed in buffers that have been allocated by the network. The bus and branch objects specify how large the buffers need to be by implementing the function
virtual int getXCBufSize()
This function must return the same value for all buses and all branches in the same bus or branch classes. Buses can return a different value than branches. For example, a power flow calculation, it is necessary that ghost buses get new values of the phase and voltage magnitude increments. These are both real numbers so the getXCBusSize routine needs to return the value 2*sizeof(double). Note that all buses must return this value even if the bus is a reference bus and does not participate in the calculation.
This function is queried by the network and used to allocate a buffer of the appropriate size. The network then informs the bus and branch objects where the location of the buffer is by invoking the function
virtual void setXCBuf(void *buf)
The bus or branch can use this function to set internal pointers to this buffer that can be used to assign values to the buffer (which is done before a ghost exchange) or to collect values from the buffer (which is done after a ghost exchange). Continuing with the powerflow example, the bus implemention of the setXCBuf function would look like
setXCBuf(void *buf)
{
p_Ang_ptr = (double*)buf;
p_Mag_ptr = p_Ang_ptr;
}
The pointers p_Ang_ptr and p_Mag_ptr are internal variables of the bus implementation and can be used elsewhere in the bus whenever the voltage angle and voltage magnitude variables are needed. After a network update operation, ghost buses will contain values for these variables that were calculated on the home processor that owns the corresponding bus.
The BaseBusComponent and BaseBranchComponent classes contain a few additional functions that are specific to whether or not a component is a bus or a branch. The BaseBusComponent class contains functions that can be used to identify attached buses or branches, determine if the bus is a reference bus, and recover the original indices of the bus. Other functions are included in the BaseBusClass but these are not usually required by application developers.
To get a list of pointers to all branches connected to a bus, the function
void getNeighborBranches(std::vector<boost::shared_ptr<BaseComponent> > &nghbrs) const
can be called. This provides a list of all pointers that have the bus as one of it endpoints. This can be used inside a bus method to loop over attached branches, which is a common motif in matrix calculations. For example, to evaluate the contribution to a diagonal element of the Y-matrix coming from transmission lines, it is necessary to perform the sum
Y_ii=-∑_(j≠i)▒Y_ij
where the Yij are the contribution due to transmission lines from the branch connecting i and j. The code inside a bus component that evaluates this sum can be written as
std::vector<boost::shared_ptr<BaseComponent> > branches;
getNeighborBranches(branches);
ComplexType y_diag(0.0,0.0);
for (int i=0; i<branches.size(); i++) {
PFBranch *branch = dynamic_cast<PFBranch*>(branches[i].get());
Y_diag += branch->getYContribution();
}
</pre></code>
The function getYContribution evaluates the quantity Yij using parameters that are local to the branch. The return value is then accumulated into the bus variable y_diag, which is eventually returned through the matrixDiagValues function. The dynamic_cast is necessary to convert the pointer from a BaseComponent object to the application class PFBranch. The BaseComponent class has no knowledge of the getYContribution function, this is only implemented in PFBranch.
A function that is similar to getNeighborBranches is
void getNeighborBuses(std::vector<boost::shared_ptr<BaseComponent> > &nghbrs) const
which can be used to get a list of the buses that are connected to the calling bus via a single branch.
Many power grid problems require the specification of a special bus as a reference bus. This designation can be handled by the two functions
void setReferenceBus(bool status) bool getReferenceBus() const
The first function can be used (if called with the argument true) to designate a bus as the reference bus and the second function can be called to inquire whether a bus is the reference bus.
Finally, it is often useful for exporting results if the original index of the bus is available. This can be recovered using the function
int getOriginalIndex() const
This function only works correctly after a call to the base factory method setComponents. Other functions in the BaseBusComponent class are needed within the framework but are not usually required by application developers.
The BaseBranchComponent class is similar to the BaseBusComponent class and provides basic information about branches and the buses at either end of the branch. To retrieve pointers to the buses at the ends of the branch, the following two functions are available
boost::shared_ptr<BaseComponent> getBus1() const boost::shared_ptr<BaseComponent> getBus2() const
The getBus1 function returns a pointer to the “from” bus, the getBus2 function returns a pointer to the “to” bus.
Two other functions in the BaseBranchComponent class that are useful for writing output are
int getBus1OriginalIndex() const int getBus2OriginalIndex() const
Like the getOriginalIndex function for the BaseBusComponent class, these functions will not work correctly until the setComponents method has been called in the base factory class.
Finally, a separate network component class that is associated with all buses and branches (including ghost buses and branches) is the DataCollection class. This class is a simple container that can be used to store key-value pairs. It also resides in the gridpack::component namespace and uses the gridpack/component/data_collection.hpp header file. When the network is created using a standard parser to read a network configuration file (see more on parsers below), each bus and branch in the network, including the ghosts, has an associated DataCollection object that contains all parameters from the configuration file that are associated with a particular bus or branch. These can be retrieved from the DataCollection object using some simple accessors. Data can be stored in two ways inside the DataCollection object. The first method assumes that there is only a single instance of the key-value pair, the second assumes there are multiple instances. This second case can occur, for example, if there are multiple generators on a bus. Generators are characterized by a collection of parameters and each generator has its own set of parameters. The generator parameters can be indexed so that they can be matched with a specific generator.
Assuming that a parameter only appears once in the data collection, the contents of a DataCollection object can be accessed using the functions
bool getValue(char *name, int *value) bool getValue(char *name, long *value) bool getValue(char *name, bool *value) bool getValue(char *name, std::string *value) bool getValue(char *name, float *value) bool getValue(char *name, double value) bool getValue(char *name, ComplexType *value)
These functions return true if a variable of the correct type is stored in the DataCollection object with the key “name”, otherwise it returns false.
If the variable is stored multiple times in the DataCollection, then it can be accessed with the functions
bool getValue(char *name, int *value, int idx) bool getValue(char *name, long *value, int idx) bool getValue(char *name, bool *value, int idx) bool getValue(char *name, std::string *value, int idx) bool getValue(char *name, float *value, int idx) bool getValue(char *name, double value, int idx) bool getValue(char *name, ComplexType *value, int idx)
where idx is an index that identifies a particular instance of the key. These functions are used primarily to implement the network component load method, described in the next section.
Network Component Factory: : the network component factory is an application-dependent piece of software that is designed to manage interactions between the network and the network component objects. Most operations in the factory run over all buses and all branches and invoke some operation on each bus and each branch. An example is the “load” operation. After the network is read in from an external file, it consists of a topology and a set of simple data collection objects containing key-value pairs associated with each bus and branch. The load operation then runs over all buses and branches and instantiates the appropriate objects by invoking a load method in each branch and bus object that takes the values from the data collection object and uses it to instantiate the bus or branch. The application network factory is derived from a base network factory class that contains some additional routines that set up indices, assign neighbors (which initially are only known by the network) to individual buses and branches and assign buffers. The network component factory may also execute other routines that contribute to setting up the network and creating a well-defined state.
Factories can be derived from the BaseFactory class, which is a templated class that based on the network type. It resides in the gridpack::factory namespace and uses the gridpack/factory/base_factory.hpp header file. The BaseFactory class supplies some basic functions that can be used to help instantiate the components in a network. Others can be added for particular applications by subclassing the BaseFactory class. The two most important functions in the BaseFactory class are
virtual void setComponents() virtual void setExchange()
The setComponents method pushes topology information available from the network into the individual buses and branches using methods in the base network class. This operation ensures that operations such as getNeighborBuses, etc. in the base network component classes work correctly. The topology information is originally only available in the network and it requires additional operations to make available to individual buses and branches. However, having this information imbedded in the buses and branches themselves can simplify application programming substantially.
The setExchange function allocates buffers and sets up pointers in the components so that exchange of data between buses and branches can occur and ghost buses and branches can receive updated values of the exchanged parameters. This functions loops over the getXCBusSize and setXCBuf commands defined in the network component classes and guarantees that buffers are properly allocated and exposed to the network components.
Two other functions are defined in the BaseFactory class as convenience functions. The first is
virtual void load()
This function loops over all buses and branches and invokes the individual bus and branch load methods. This moves information from the DataCollection objects that are instantiated when the network is created from a network configuration file to the bus and branch objects themselves. The second convenience function is
virtual void setMode(int mode)
This function loops over all buses and branches in the network and invokes each bus and branches load method. It can be used to set the behavior of the entire network in single function call.
Mapper: the mapper is a generic capability that can be used to generate a matrix or vector from the network components. This is done by running over all the network components and invoking methods in the matrix-vector interface. The mapper is basically a transformation that converts a set of network components into a matrix or vector based on the behavior of their matrix-vector interfaces. It has no explicit dependencies on either the network components or the type of analyses being performed so this capability is applicable across a wide range of problems.
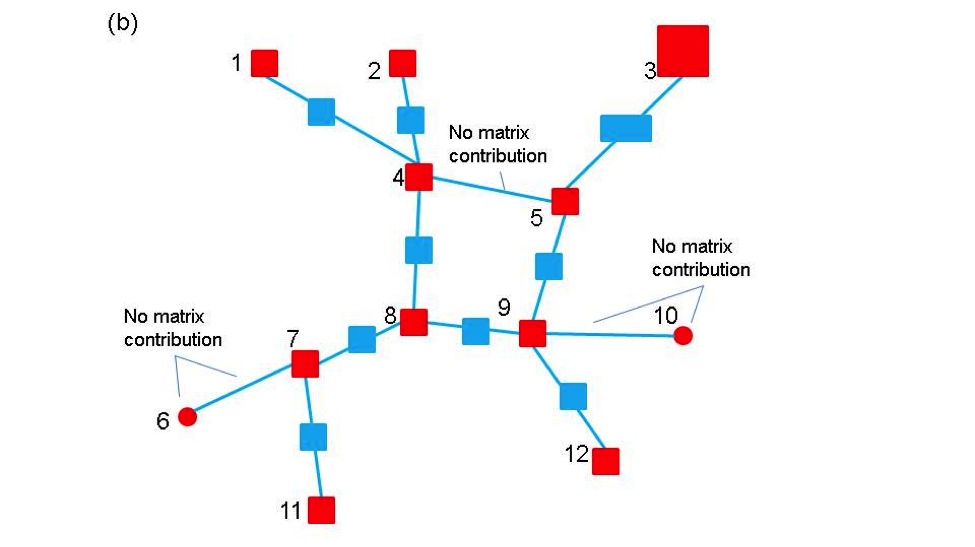
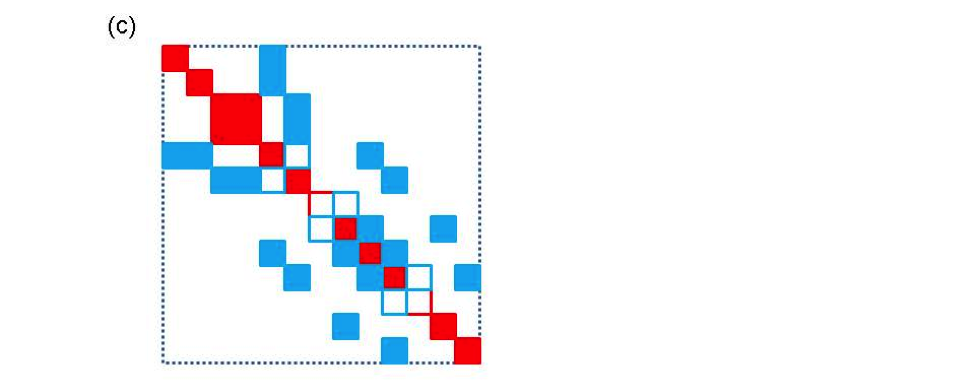
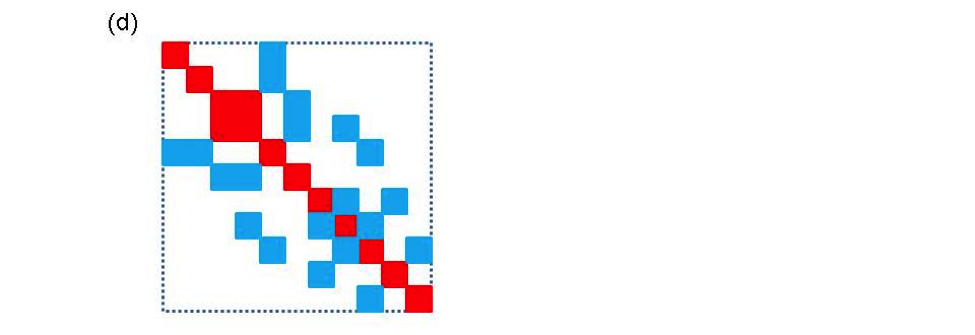
The matrix-vector interface contains functions that provide two pieces of information about each network component. The first is the size of the matrix block that is contributed by the component and the second is the values in that block. Using this information, the mapper can figure out what the dimensions of the matrix are and where individual elements in the matrix are located. The construction of matrix by the mapper is illustrated in Figure 4 for a small network. Figure 4(a) shows a hypothetical network for which some buses and branches do not contribute to the matrix, as seen in Figure 4(b). This could occur in real systems because the transmission line corresponding to the branch has failed or because a bus represents the reference bus. In addition, it is not necessarily true that all buses and branches contribute the same size elements. The mapping of the individual contributions from the network in Figure 4(b) to initial matrix locations is shown in Figure 4(c). This is followed by elimination of gaps in the matrix in Figure 4(d).
Figure 4. A schematic diagram of the matrix map function. The bus numbers in (a) and (b) map to approximate row and column locations in (c). (a) a small network (b) matrix blocks associated with branches and buses. Not that not all blocks are the same size and not all buses and branches contribute (c) initial construction of matrix based on network indices (d) final matrix after eliminating gaps
The most complex part of generating matrices and vectors is implementing the functions in the MatVecInterface. Actually creating matrices and vectors using the mappers is quite simple, once this has been done. Currently, GridPACK™ supports two mappers, one that creates matrices from buses and branches and a second that can create vectors from buses. Both mappers are templated objects based on the type of network being used and use the gridpack::mapper namespace. The FullMatrixMap object runs over both buses and branches to set up a matrix and uses the gridpack/mapper/full_map.hpp header file. The constructor is
FullMatrixMap(boost::shared_ptr<MyNetwork> network)
The network is passed in to the object via the constructor. The constructor sets up a number of internal data structures based on what mode has been set in the network components. This means that a mapper is created while the mode is set to construct the Y-matrix, then it will be necessary to instantiate a second mapper to create the Jacobian for a power flow calculation.
Once the mapper has been created, a matrix can be generated using the call
boost::shared_ptr<gridpack::math::Matrix> mapToMatrix()
This function creates a new matrix and returns a pointer to it. If a matrix already exists and it is only necessary to update the values, then the functions
void mapToMatrix( boost::shared_ptr<gridpack::math::Matrix &matrix) void mapToMatrix(gridpack::math::Matrix &matrix)
can be used. These functions use the existing matrix data structures and overwrite the values of individual elements. For these to work, it is necessary to use the same mapper that was used to create the original matrix and to have the same mode set in the network components.
The vector mapper works in an entirely analogous way to the matrix mapper and uses the gridpack/mapper/bus_vector_map.hpp header file. The constructor for the BusVectorMap class is
BusVectorMap(boost::shared_ptr<MyNetwork>)
And the function for build a new vector is
boost::share_ptr<gridpack::math::Vector mapToVector()
The functions for overwriting the values of an existing vector are
void mapToVector(boost::shared_ptr<gridpack::math::Vector &vector) void mapToVector(gridpack::math::Vector &vector)
The vector map can also be used to write values back to buses using the function
void mapToBus(const gridpack::math::Vector &vector)
This function will copy values from the vector into the bus using the setValues function in the MatVecInterface.
Import Module: the import module is designed to read an external network file, set up the network topology and assign any parameter fields in the file to simple fields. The import module does not partition the network, it is only responsible for reading in the network and distributing the different network elements in a way that guarantees that not too much data ends up on any one processor. The import module is also not responsible for determining if the input is compatible with the analysis being performed. This can be handled by the network factory. The import module is only responsible for determining if it can read the file.
Currently, GridPACK™ only supports one file format and there is only one parser. Files based on the PSS/E PTI version 23 format can be read in using the class PTI23_parser. This is another templated class that uses the network type as a template argument. PTI23_parser is located in the gridpack::parser namespace and uses the gridpack/parser/PTI23_parser.hpp header file. This class has only two important functions. The first is the constructor
PTI23_parser(boost::shared_ptr<MyNetwork> network)
and the second is the function
void parse(const std::string &filename)
where filename refers to the location of the network configuration file. To use this parser, network object with the right bus and branch classes is instantiated and then passed to the constructor of the PTI23_parser. The parse method is then invoked with the location of the network configuration file and the network is filled out with buses and branches. The parameters in the network configuration file are stored as key-value pairs in the DataCollection object associated with each bus and branch. Once the partition method has been called on the network the network is fully distributed with ghost buses and branches in place and other operations can be performed.
Another key part of the parsing capability is the dictionary.hpp file, which is designed to provide a common nomenclature for parameters associated with power grid component. It is also the key to extracting parameters from the DataCollection objects created by the parser. For example, the parameter describing the resistance of a transmission element is given the common name BRANCH_RESISTANCE. This string is defined as a macro in the dictionary.hpp file as
#define BRANCH_RESISTANCE “BRANCH_RESISTANCE”
The macro is used in all function calls that reference this variable by name. The use of a macro provides compile time error checking on the name. The goal of using the dictionary is that all parsers will eventually store the branch resistance parameter in the DataCollection object using this common name. Applications can then switch easily between different network configuration file formats by simply exchanging parsers, which will all store corresponding parameters using a common naming convention.
Serial IO Module: the serial IO module is designed to provide a simple mechanism for writing information from selected buses and/or branches to standard output using a consistent ordering scheme. Individual buses and/or branches implement a write method that will write bus/branch information to a single string. This information usually consists of bus or branch identifiers plus some parameters that are desired in the output. The serial IO module then gathers this information, moves it to the head node, and writes it out in a consistent order. An example of this type of output is shown below.
Bus Voltages and Phase Angles
Bus Number Phase Angle Voltage Magnitude
1 0.000000 1.060000
2 -4.980000 927.649818
3 -12.720000 280.919266
4 -10.330000 -1437.822431
5 -8.780000 -1320.922177
6 -14.220000 548.139123
7 -13.370000 -790.995324
8 -13.360000 189.293173
9 -14.940000 -971.618443
10 -15.100000 -589.181023
11 -14.790000 -345.309479
12 -15.070000 -223.066355
13 -15.160000 -426.487761
14 -16.040000 -211.325836
Figure 5. Example output from buses in a 14 bus problem.
Like the mapper, the serial IO classes are relatively easy to use. Most of the complexity is associated with implementing the serialWrite methods in the buses and branches. Data can be written out for buses and/or branches using either the SerialBusIO class or the SerialBranchIO class. These are again templated classes that take the network as an argument in the constructor. Both classes reside in the gridpack::serial_io namespace and use the gridpack/serial_io/serial_io.hpp header file The SerialBusIO constructor has the form
SerialBusIO(int max_str_len, boost::shared_ptr<MyNetwork> network)
The variable max_str_len is the length, in bytes, of the maximum size string you would want to write out using this class and network is a pointer to the network that is used to generate output. Two additional functions can be used to actually generate output. They are
void header(const char *string) const
and
void write(const char *signal = NULL)
The header method is a convenience function that will only write the buffer string from the head processor (process 0) and can be used for creating the headings above an output listing. The write function traverses all the buses in the network and writes out the strings generated by the serialWrite methods in the buses. The SerialBusIO object is responsible for reordering these strings in a consistent manner, even if the buses are distributed over many processors. The optional variable “signal” is passed to the serialWrite methods and can be used to control what output is listed. For example, in one part of a simulation it might be desirable to list the voltage magnitude and phase angle from a powerflow calculation and in another part of the calculation to list the rotor angle for a generator. These two outputs could be distinguished from each other in the serialWrite function using the signal variable.
To generate the output in Figure 6, the following calls are used
gridpack::serial_io::SerialBusIO<MyNetwork> busIO(128,network);
busIO.header("\n Bus Voltages and Phase Angles\n");
busIO.header(
"\n Bus Number Phase Angle Voltage Magnitude\n");
busIO.write();
The first call creates the SerialIOBus object and specifies the internal buffers size (128 bytes). This buffer must be large enough to incorporate the output from any call to one of the serialWrite calls in the bus components. The next two lines print out the header on top of the bus listing and the last line generates the listing itself. The serialWrite implementation looks like
bool gridpack::myapp::MyBus::serialWrite(char *string,
const char *signal)
{
double pi = 4.0*atan(1.0);
double angle = p_a*180.0/pi;
sprintf(string, " %6d %12.6f %12.6f\n",
getOriginalIndex(),angle,p_v);
}
For this simple case, the signal is ignored. If more than one type of bus listing was desired, additional conditions based on the value of signal could be included.
The SerialBranchIO module is similar to the SerialBusIO module but works by creating listings for branches. The constructor is
SerialBranchIO(int max_str_len, boost::shared_ptr<MyNetwork> network)
and the header and write methods are
void header(const char *string) const void write(const char *signal = NULL)
These have exactly the same behavior as in the SerialBusIO class.
Configuration Module: the configuration module is designed to provide a central mechanism for directing module specific information to each of the components making up a given application. For example, information about convergence thresholds and maximum numbers of iterations might need to be picked up by the solver module from an external configuration file. The configuration module is designed to read input files using a simple XML format that supports a hierarchical input. This can be used to control which input gets directed to individual objects in the application, even if the object is a framework component and cannot be modified by the application developer.
The configuration module declared in configuration.hpp and public methods are in class gridpack::utility::Configuration. The static method configuration() returns a pointer to the shared instance of this classed used by all modules in an application. This function is initialized once:
gridpack::utility::Configuration * c = gridpack::utility::Configuration::configuration() ; c->open(input_file, MPI_COMM_WORLD);
The input file uses XML markup syntax. The single top-level element must be named “Configuration” but other elements may have module and application specific names. Refer elsewhere in this document for specifics. For illustration only, an example configuration file might look like:
<?xml version="1.0" encoding="utf-8"?>
<Configuration>
<PowerFlow>
<networkConfiguration> IEEE14.raw </networkConfiguration>
</PowerFlow>
<DynamicSimulation>
<StartTime> 0.0 </StartTime>
<EndTime> 0.1 </EndTime>
<TimeStep> 0.001 </TimeStep>
<Faults>
<Fault>
<StartFault> 0.03 </StartFault>
<EndFault> 0.06 </EndFault>
<Branch> 3 7 </Branch>
</Fault>
<Fault>
<StartFault> 0.07 </StartFault>
<EndFault> 0.06=8 </EndFault>
<Branch> 4 8 </Branch>
</Fault>
</Faults>
</DynamicSimulation>
</Configuration>
A value in this configuration file is accessed with a call to the overloaded method get(). For example:
std::string s =
c->get("Configuration.PowerFlow.networkConfiguration",
"No network configuration specified");
The first argument has type Configuration::KeyType which is a typedef of std::string. Values are selected by hierarchically named “keys” using “.” as a separator. There are overloads of get() for accessing C++ types: bool, int, double, and std::string. For each type there are two variants. For integers these look like
int get(const KeyType &, int default_value)const ; bool get(const KeyType &, int *) const;
The first variant takes a key name and a default value and returns the value in the configuration file or the default value when none is specified. In the second variant, a Boolean value is returned indicating if the value was in the configuration file and the second argument pointers an object that is updated with the configuration value when it is present. For strings, the second argument is passed by reference.
There is also a pair of overloads that support the type std::vector<double> which are used to access three-vectors where components are separately named child elements X, Y, and Z.
The method getCursor(KeyType) returns a pointer to an internal element in the hierarchy. This “cursor” supports the same get() methods as above but the names are now relative to the name of the cursor. Thus we might modify the previous example to:
Configuration::CursorPtr p =
c->getCursor("Configuration.PowerFlow");
std::string s = p->get("networkConfiguration",
"No network configuration specified");
An additional use of such cursors is to access lists of values. The method
typedef std::vector<CursorPtr> ChildCursors; void children(ChildCursors &);
can be used to get a vector of all the elements that are children in the name hierarchy of some element. These children need not have unique names as illustrated by the children of the “Faults” element shown above. In this example, each of the children is a cursor that can be used to access “StartFault”, “EndFault”, and “Branch” parameters.
Developing Applications
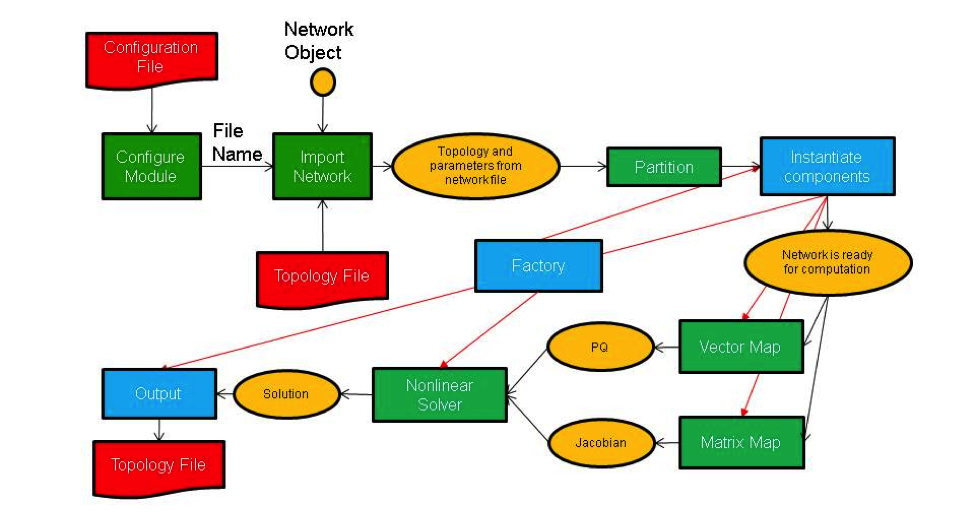
The use of these modules in an application such as power flow is outlined in Figure 6. For different power grid problems, the details of the code will be different, but most of these motifs will appear at some point or other. The main differences will probably be in feedback loops as results from one part of the calculation are fed back into other parts of the calculation. For example, an iterative solver will likely need to update the current values of the network components, which can then be used to generate new matrices and vectors that are fed back into the next iteration of the solver. The diagram is not complete, but gives an overall view of code structure and data movement.
Figure 6. Schematic of program flow for a power flow simulation. The yellow ovals are distributed data objects, the green blocks are GridPACK™ framework components and the blue blocks are application specific code. External files are red.
As shown in the figure, application developers will need to focus on writing two or three sets of modules. The first is the network components. These are the descriptions of the physics and/or measurements that are associated with buses and branches in the power grid network. The network factory is a module that initializes the grid components on the network after the network is originally created by the import module. The power flow problem is simple enough that it can use a non-linear solver directly from the math module but even a straightforward solution such as this requires the developer to overwrite some functions in the factory that are used in the non-linear solver iterations.
Most of the work involved in creating a new application focuses on creating the bus and branch classes for the application. This discussion will focus on creating a code to perform power flow calculations of an electric network and will describe in some detail the routines that need to be written in order to develop a working simulation. This application has been included as part of the GridPACK™ distribution and users are encouraged to look at the source code. The discussion below is designed to illustrate how to build an application and for brevity has left out some calculations compared to the working implementation. The source code also contains more comment lines as well as some additional diagnostics that may not appear here. However, the overall design is the same and readers who have a good understanding of the following text should have no difficulty understanding the powerflow source code.
For the power flow calculation, the buses and branches will be represented by the classes PFBus and PFBranch. PFBus inherits from the BaseBusComponent class, so it automatically inherits the BaseComponent and MatVecInterface classes as well. The first thing that must be done in creating the PFBus component is to overwrite the load function in the BaseComponent class. The original function is just a placeholder that performs no action. The load function should take parameters from the DataCollection object associated with each bus and use them to initialize the bus component itself. For the PFBus component, a simplified load function is
void gridpack::powerflow::PFBus::load(
const boost::shared_ptr<gridpack::component
::DataCollection> &data)
{
data->getValue(CASE_SBASE, &p_sbase);
data->getValue(BUS_VOLTAGE_ANG, &p_angle);
data->getValue(BUS_VOLTAGE_MAG, &p_voltage);
p_v = p_voltage;
double pi = 4.0*atan(1.0); p_angle = p_angle*pi/180.0;
p_a = p_angle;
int itype; data->getValue(BUS_TYPE, &itype);
if (itype == 3) {
setReferenceBus(true);
}
bool lgen;
int i, ngen, gstatus;
double pg, qg;
if (data->getValue(GENERATOR_NUMBER, &ngen)) {
for (i=0; i<ngen; i++) {
lgen = true;
lgen = lgen && data->getValue(GENERATOR_PG, &pg,i);
lgen = lgen && data->getValue(GENERATOR_QG, &qg,i);
lgen = lgen && data->getValue(GENERATOR_STAT, &gstatus,i);
if (lgen) {
p_pg.push_back(pg);
p_qg.push_back(qg);
p_gstatus.push_back(gstatus);
}
}
}
}
This version of the load function has left off additional properties, such as shunts and loads and some transmission parameters, but it serves to illustrate how load is suppose to work. The load method in the base factory class will run over all buses, get the DataCollection object associated with that bus and then call the PFBus::load method for that bus using the DataCollection object as the argument. The parameters p_sbase, p_angle, p_voltage are private members of PFBus. The variables corresponding to the keys CASE_SBASE, BUS_VOLTAGE_ANG, BUS_VOLTAGE_MAG were stored in the DataCollection object when the network configuration file was parsed. They are retrieved from this object using the getValue functions and assigned to p_sbase, p_angle, p_voltage. Additional internal variables are also assigned in a similar manner. The value of the BUS_TYPE variable can be used to determine whether the bus is a reference bus. Note that the CASE_SBASE etc. are just preprocessor symbols that are defined in the dictionary.hpp file, which must be included in the file defining the load function.
The variables referring to generators have a different behavior than the other variables. A bus can have multiple generators and these are stored in the DataCollection object with an index. The number of generators is also stored in the DataCollection object with the key GENERATOR_NUMBER. First the number of generators is retrieved and then a loop is set up so all the generator variables can be accessed. These are stored in local vectors. The generator parameters are stored in local private arrays. The loop shows how the return value of the getValue function can be used to verify that all three parameters for a generator where found. If they aren’t found, then the generator is incomplete and the generator is not added to the local data. This can also be used to determine if the bus has other properties and to set internal flags and parameters accordingly. The load function for the PFBranch is constructed in a similar way, except that the focus is on extracting branch related parameters from the DataCollection object.
Both the PFBus and PFBranch classes contain an application-specific function called setYBus that is used to set up values in the Y-matrix. There is also a function in the powerflow factory class that runs over all buses and branches and calls this function. The setYBus function in PFBus is
void gridpack::powerflow::PFBus::setYBus(void)
{
gridpack::ComplexType ret(0.0,0.0);
std::vector<boost::shared_ptr<BaseComponent> > branches;
getNeighborBranches(branches);
int size = branches.size();
int i;
for (i=0; i<size; i++) {
gridpack::powerflow::PFBranch *branch
= dynamic_cast<gridpack::powerflow::PFBranch*>
(branches[i].get());
ret -= branch->getAdmittance();
ret -= branch->getTransformer(this);
ret += branch->getShunt(this);
}
if (p_shunt) {
gridpack::ComplexType shunt(p_shunt_gs,p_shunt_bs);
ret += shunt;
}
p_ybusr = real(ret);
p_ybusi = imag(ret);
}
This function evaluates the contributions to the Y-Matrix associated with buses. The real and imaginary parts of this number are stored in the internal variables p_ybusr and p_ybusi. The subroutine first creates the local variable ret and then gets a list of pointers to neighboring branches from the BaseBusComponent function getNeighborBranches. The function then loops over each of the branches and casts the BaseComponent pointer from the list to a PFBranch pointer. The getAdmittance, getTransformer and getShunt methods return the contributions from simple transmission elements, transformers and shunts associated with the branch. These are accumulated into the ret variable. Note that some parameters, such as p_shunt, are set in the full PFBus::load method but not in the truncated version discussed above.
The reason that the getAdmittance variable has no argument while both getTransformer and getShunt take the pointer “this” as an argument is that the contribution from simple transmission elements is symmetric for both the “from” and “to” buses while the transformer and shunt contributions are not. This can be seen by examining the getTransformer function.
gridpack::ComplexType
gridpack::powerflow::PFBranch::getTransformer(
gridpack::powerflow::PFBus *bus)
{
gridpack::ComplexType ret(p_resistance,p_reactance);
if (p_xform) {
ret = -1.0/ret;
gridpack::ComplexType a(cos(p_phase_shift),sin(p_phase_shift));
a = p_tap_ratio*a;
if (bus == getBus1().get()) {
ret = ret/(conj(a)*a);
} else if (bus == getBus2().get()) {
// ret is unchanged
}
} else {
ret = gridpack::ComplexType(0.0,0.0);
}
return ret;
}
The variables p_resistance, p_reactance, p_phase_shift, and p_tap_ratio are all internal variables that are set based on the variables read in from using the load method or are set in other initialization steps. The boolean variable p_xform variable is set to true in the PFBranch::load method if transformer related variables are detected in the DataCollection objects associated with the branch, otherwise it is false.
The PFBranch version of the setYBus function is
void gridpack::powerflow::PFBranch::setYBus(void)
{
gridpack::ComplexType ret(p_resistance,p_reactance);
ret = -1.0/ret;
gridpack::ComplexType a(cos(p_phase_shift),sin(p_phase_shift));
a = p_tap_ratio*a;
if (p_xform) {
p_ybusr_frwd = real(ret/conj(a));
p_ybusi_frwd = imag(ret/conj(a));
p_ybusr_rvrs = real(ret/a);
p_ybusi_rvrs = imag(ret/a);
} else {
p_ybusr_frwd = real(ret);
p_ybusi_frwd = imag(ret);
p_ybusr_rvrs = real(ret);
p_ybusi_rvrs = imag(ret);
}
gridpack::powerflow::PFBus *bus1 =
dynamic_cast<gridpack::powerflow::PFBus*>(getBus1().get());
gridpack::powerflow::PFBus *bus2 =
dynamic_cast<gridpack::powerflow::PFBus*>(getBus2().get());
p_theta = (bus1->getPhase() - bus2->getPhase());
}
Note that the branch version of the setYBus function calculates different values for the Y-matrix contribution depending on whether the first index in the matrix element corresponds to bus 1 (the forward direction) or bus 2 (the reverse direction). These are stored in the separate variables p_ybusr_frwd and p_ybusi_frwd for the forward directions and p_ybusr_rvrs and p_ybusi_rvrs for the reverse direction. This routine also calculates the variable p_theta which is equal to the difference in the phase angle variable associated with the two buses at either end of the branch. This last variable provides an example of calculating a branch parameter based on the values of parameters located on the terminal.
The setYBus functions are used in the powerflow components to set some basic parameters. These are eventually incorporated into the Jacobian matrix and PQ vector that constitute the matrix and right hand side vector of the powerflow equations. To build the matrix, it is necessary to implement the matrix size and matrix values functions in the MatVecInterface. The functions for setting up the matrix are discussed in detail in the following, the vector functions are simpler but follow the same pattern. The mode used for setting up the Jacobian matrix is “Jacobian”. The corresponding matrixDiagSize routine is
bool gridpack::powerflow::PFBus::matrixDiagSize(int *isize,
int *jsize) const
{
if (p_mode == Jacobian) {
*isize = 2;
*jsize = 2;
return true;
} else if (p_mode == YBus) {
*isize = 1;
*jsize = 1;
return true;
}
}
This function handles two modes, stored in the internal variable p_mode. If the mode equals Jacobian, then the function returns a contribution to a 2×2 matrix. In the case that the mode is “YBus” the function would return a contribution to a 1×1 matrix. (The Jacobian is treated as a real matrix where the real and complex parts of the problem are treated as separate variables, the Y-matrix is handle as a regular complex matrix). The corresponding code for returning the diagonal values is
bool gridpack::powerflow::PFBus::matrixDiagValues(ComplexType *values)
{
if (p_mode == YBus) {
gridpack::ComplexType ret(p_ybusr,p_ybusi);
values[0] = ret;
return true;
} else if (p_mode == Jacobian) {
if (!getReferenceBus()) {
values[0] = -p_Qinj - p_ybusi * p_v *p_v;
values[1] = p_Pinj - p_ybusr * p_v *p_v;
values[2] = p_Pinj / p_v + p_ybusr * p_v;
values[3] = p_Qinj / p_v - p_ybusi * p_v;
if (p_isPV) {
values[1] = 0.0;
values[2] = 0.0;
values[3] = 1.0;
}
return true;
} else {
values[0] = 1.0;
values[1] = 0.0;
values[2] = 0.0;
values[3] = 1.0;
return true;
}
}
}
This function also handles two modes based on the enumerated types “Jacobian” and “YBus”. If the mode is “YBus”, the function returns a single complex value. If the mode is “Jacobian”, the function checks first to see if the bus is a reference bus or not. If the bus is not a reference bus, then the function returns a 2×2 block corresponding to the contributions to the Jacobian matrix coming from a bus element. If the bus is a reference bus, the function returns a 2×2 identity matrix. This is a result of the fact that the variables associated with a reference bus are fixed. In fact, the variables contributed by the reference bus could be eliminated from the matrix entirely by returning false if the mode is “Jacobian” and the bus is a reference bus for both the matrix size and matrix values routines. This would also require some adjustments to the off-diagonal routines as well. There is an additional condition for the case where the bus is a “PV” bus. In this case one of the independent variables is eliminated by setting the off-diagonal elements of the block to zero and the second diagonal element equal to 1.
The matrixForwardSize and matrixForwardValues routines, as well as the corresponding Reverse routines, are implemented in the PFBranch class. These functions determine the off-diagonal blocks of the Jacobian and Y-matrix. The matrixForwardSize routine is given by
bool gridpack::powerflow::PFBranch::matrixForwardSize(int *isize,
int *jsize) const
{
if (p_mode == Jacobian) {
gridpack::powerflow::PFBus *bus1
= dynamic_cast<gridpack::powerflow::PFBus*>(getBus1().get());
gridpack::powerflow::PFBus *bus2
= dynamic_cast<gridpack::powerflow::PFBus*>(getBus2().get());
bool ok = !bus1->getReferenceBus();
ok = ok && !bus2->getReferenceBus();
if (ok) {
*isize = 2;
*jsize = 2;
return true;
} else {
return false;
}
} else if (p_mode == YBus) {
*isize = 1;
*jsize = 1;
return true;
}
}
If the mode is “YBus”, the size function returns a 1×1 block for the off-diagonal matrix block. For the Jacobian, the function first checks to see if either end of the branch is a reference bus by evaluating the Boolean variable “ok”. If neither end is the reference bus then the function returns a 2×2 block, if one end is the reference bus then the function returns false. The false value indicates that this branch does not contribute to the matrix. For this system, the matrixReverseSize function is the same, but if the off-diagonal contributions were not square blocks, then the dimensions of the blocks would need to be switched.
The matrixForwardValues function is
bool gridpack::powerflow::PFBranch::matrixForwardValues(
ComplexType *values)
{
if (p_mode == Jacobian) {
gridpack::powerflow::PFBus *bus1
= dynamic_cast<gridpack::powerflow::PFBus*>(getBus1().get());
gridpack::powerflow::PFBus *bus2
= dynamic_cast<gridpack::powerflow::PFBus*>(getBus2().get());
bool ok = !bus1->getReferenceBus();
ok = ok && !bus2->getReferenceBus();
if (ok) {
double cs = cos(p_theta);
double sn = sin(p_theta);
values[0] = (p_ybusr_frwd*sn - p_ybusi_frwd*cs);
values[1] = (p_ybusr_frwd*cs + p_ybusi_frwd*sn);
values[2] = (p_ybusr_frwd*cs + p_ybusi_frwd*sn);
values[3] = (p_ybusr_frwd*sn - p_ybusi_frwd*cs);
values[0] *= ((bus1->getVoltage())*(bus2->getVoltage()));
values[1] *= -((bus1->getVoltage())*(bus2->getVoltage()));
values[2] *= bus1->getVoltage();
values[3] *= bus1->getVoltage();
bool bus1PV = bus1->isPV();
bool bus2PV = bus2->isPV();
if (bus1PV & bus2PV) {
values[1] = 0.0;
values[2] = 0.0;
values[3] = 0.0;
} else if (bus1PV) {
values[1] = 0.0;
values[3] = 0.0;
} else if (bus2PV) {
values[2] = 0.0;
values[3] = 0.0;
}
return true;
} else {
return false;
}
} else if (p_mode == YBus) {
values[0] = gridpack::ComplexType(p_ybusr_frwd,p_ybusi_frwd);
return true;
}
}
For the “YBus” mode, the function simply returns the complex contribution to the Y-matrix. For the “Jacobian” mode, the function first determines if either end of the branch is connected to the reference bus. If it is, then function returns false and there is no contribution to the Jacobian. If neither end of the branch is the reference bus then the function evaluates the 4 elements of the 2×2 contribution to the Jacobian coming from the branch. To do this, the branch needs to get the current values of the voltages on the buses at either end. It can do this by using the getVoltage accessor functions that have been defined in the PFBus class. Finally, if one end or the other of the branch is a PV bus, then some variables need to be eliminated from the equations. This can be done by setting some of the values in the 2×2 block equal to zero.
The matrixReverseValues function is similar to the matrixForwardValues functions with a few key differences. 1) the variables p_ybusr_rvrs and p_ybusi_rvrs are used instead of p_ybusr_frwd and p_ybusi_frwd 2) instead of using cos(p_theta) and sin(p_theta) the function uses cos(-p_theta) and sin(-p_theta) since p_theta is defined as difference in phase angle on bus 1 minus the difference in phase angle on bus 2 and 3) the values that are set to zero in the conditions for PV buses are transposed. The PV conditions are the same as the forward case if both bus 1 and bus 2 are PV buses, if only bus 1 is a PV bus then values[2] and values[3] are zero and if only bus2 is a PV bus then values[1] and values[3] are zero.
The functions for setting up vectors are similar to the corresponding matrix functions, although they are a bit simpler. The vector part of the MatVecInterface contains one function that does not have a counterpart in the set of matrix functions and that is the setValues function. This function can be used to push values in a vector object back into the buses that were used to generate the vector. For the Newton-Raphson iterations used to solve the powerflow equations, it is necessary at each iteration to push the current solution back into the buses so they can be used to evaluate new Jacobian and right hand side vectors. The solution vector contains the current increments to the voltage and phase angle. These are written back to the buses using the function
void gridpack::powerflow::PFBus::setValues(
gridpack::ComplexType *values)
{
p_a -= real(values[0]);
p_v -= real(values[1]);
*p_vAng_ptr = p_a;
*p_vMag_ptr = p_v;
}
This function is paired with a mapper that is used to create a vector with the same pattern of contributions. If for example, the matrix equation Ax = b is being solved, then the mapper used to create the right hand side vector b should be used to push results back onto the buses using the mapToBus method. The setValues method above takes the contributions from the solution vector and uses then to decrement the internal variables p_a (voltage angle) and p_v (voltage magnitude). The new values of p_a and p_v are then assigned to the buffers p_vAng_ptr and p_vMag_ptr so that they can be exchanged with other buses. This is discussed below.
The two routines that need to be created in the PFBus class to copy data to ghost buses are both simple. There is no need to create corresponding routines in the PFBranch class since branches do not need to exchange data. Two values need to be exchanged between buses, the current voltage angle and the current voltage magnitude. This requires a buffer that is the size of two doubles so the getXCBufSize function is written as
int gridpack::powerflow::PFBus::getXCBufSize(void)
{
return 2*sizeof(double);
}
The setXCBuf assigns the buffer created in the base factory setExchange function to internal variables used within the PFBus component. It has the form
void gridpack::powerflow::PFBus::setXCBuf(void *buf)
{
p_vAng_ptr = static_cast<double*>(buf);
p_vMag_ptr = p_vAng_ptr+1;
*p_vAng_ptr = p_a;
*p_vMag_ptr = p_v;
}
The buffer created in the setExchange routine is split between the two internal pointers p_vAng_ptr and p_vMag_ptr. These are then initialized to the current values of p_a and p_v. Whenever the updateBuses routine is called the pointers on ghost buses are refreshed with the current values of these variables from the processes that own the corresponding buses. Note that both the getXCBufSize and the setXCBuf routines are only called during the setExchange routine. They are not called during the actually bus updates.
One final function in the PFBus and PFBranch class that is worth taking a brief look at is the set mode function. This function is used to set the internal p_mode variable that is defined in both classes. The PFMode enumeration, which contains both the “YBus” and “Jacobian” modes, is defined within the gridpack::powerflow namespace. The setMode function for both buses and branches has the form
void gridpack::powerflow::PFBus::setMode(int mode)
{
p_mode = mode;
}
This function is triggered on all buses and branches if the base factory setMode method is called.
Once the PFBus and PFBranch classes have been defined, it is possible to declare a PFNetwork as a typdef. This can be done using the line typedef network::BaseNetwork<PFBus, PFBranch > PFNetwork; in the header file declaring the PFBus and PFBranch classes. This type can then be used in other powerflow files that need to create objects from templated classes.
The discussion above summarizes many of the important functions in the PFBus and PFBranch classes. Additional functions are included in these classes that are not discussed here, but the basic principles involved in implementing the remaining functions have been covered.
The first part of creating a new application is writing the network component classes. The second part is to implementing the application-specific factory. For the powerflow application, this is the PFFactory class, which inherits from the BaseFactory class. Most of the important functionality in the PFFactory is derived from the BaseFactory class and is used without modification, but several application-specific functions have been added to PFFactory that are used to set internal parameters in the network components. As an example, consider the setYBus function
void gridpack::powerflow::PFFactory::setYBus(void)
{
int numBus = p_network->numBuses();
int numBranch = p_network->numBranches();
int i;
for (i=0; i<numBus; i++) {
dynamic_cast<PFBus*>(p_network->getBus(i).get())->setYBus();
}
for (i=0; i<numBranch; i++) {
dynamic_cast<PFBranch*>(p_network->getBranch(i).get())->setYBus();
}
}
This function loops over all buses and branches and invokes the setYBus method in the individual PFBus and PFBranch objects. The first two lines in the factory setYBus method grab the total number of buses and branches on the process. A loop over all buses on the process is initiated and a pointer to the bus object is obtained via the getBus bus method in the BaseNetwork class. This pointer is returned as a BaseComponent object, which doesn’t have a setYBus method so it must then be converted to a PFBus pointer which can then invoke setYBus. The same set of steps is then repeated for the branches. The factory can be used to create other methods that invoke functions on buses and/or branches. Most of these functions follow the same general form as the setYBus method just described.
The last part of building an application is creating the top level application driver that actually instantiates all the objects used in the application and controls the program flow. Running the code is broken up into two parts. The first is creating a main program and the second is creating the application driver. The main routine is primarily responsible for initializing the communication libraries and creating the application object, the application object then controls the application itself. The main program for the powerflow application is
main(int argc, char **argv)
{
int ierr = MPI_Init(&argc, &argv);
gridpack::math::Initialize();
GA_Initialize();
int stack = 200000, heap = 200000;
MA_init(C_DBL, stack, heap);
gridpack::powerflow::PFApp app; app.execute();
GA_Terminate(); gridpack::math::Finalize(); ierr = MPI_Finalize(); }
The first block of code in this program initializes the MPI and GA communication libraries and allocates internal memory used by GA. It also initializes the math libraries, which, in turn, calls the initialization routines of whatever library the math module is built on. The code then instantiates a powerflow application object and calls the execute method for this object. The remainder of the powerflow application is contained in the PFApp::execute method. Finally, when the application has finished running, the main program cleans up the communication and math libraries.
The powerflow execute method is where the top level control of the application is embedded. The execute method starts off with the code
gridpack::parallel::Communicator world; boost::shared_ptr<PFNetwork> network(new PFNetwork(world));
gridpack::utility::Configuration *config
= gridpack::utility::Configuration::configuration();
config->open("input.xml",world);
gridpack::utility::Configuration::Cursor *cursor;
cursor = config->getCursor("Configuration.Powerflow");
std::string filename = cursor->get("networkConfiguration",
"No network configuration specified");
gridpack::parser::PTI23_parser<PFNetwork> parser(network);
parser.parse(filename.c_str());
network->partition();
The first two lines create a communicator for this application and use it to instantiate a PFNetwork object (note that this is really a BaseNetwork template that is instantiated using the PFBus and PFBranch classes). The network object exists but has no buses or branches on it. The next few lines get an instance of the configuration object and use this to open the input.xml file. This filename has been hardwired into this implementation but it could be passed in as a runtime argument, if desired. The code then creates a Cursor object and initializes this to point into the Configuration.Powerflow block of the input.xml file. The cursor can then be used to get the contents of the networkConfiguration block in input.xml, which corresponds to the name of the network configuration file containing the powergrid network. After getting the file name, the code creates a PTI23_parser object and passes in the current network object as an argument. When the parse method is called, the parser reads in the file specified in filename and uses that to add buses and branches to the network object. At this point, the network has all the bus and branches from the configuration file, but no ghost buses or branches exist and buses and branches are not distributed in an optimal way. Calling the partition method on the network then distributes the buses and branches and adds appropriate ghost buses and branches.
The next set of calls initialize the network components and prepare the network for computation.
gridpack::powerflow::PFFactory factory(network); factory.load();
factory.setComponents(); factory.setExchange(); network->initBusUpdate();
factory.setYBus();
The first call creates a PFFactory object and instantiates it with a reference to the current network. The next line calls the BaseFactory load method which invokes the component load method on all buses and branches. These use data from the DataCollection objects to initialize the corresponding bus and branch objects. Note that when the partition function creates the ghost bus and branch objects, it copies the associated DataCollection objects so these parameters are available to instantiate all objects in the network. The next two methods are also implemented as BaseFactory methods. The setComponents method sets up pointers in the network components that point to neighboring branches and buses (in the case of buses) and terminal buses (in the case of branches). It is also responsible for setting up internal indices that are used by the mapper functions to create matrices and vectors. The BaseFactory setExchange method is responsible for setting up the buffers that are used to exchange data between locally owned buses and branches and their corresponding ghost images on other processors. The final factory call to setYBus evaluates the Y-matrix contributions from all network components. The network is fully initialized at this point and ready for computation.
The next set of calls create the Y-matrix and the matrices used in the Newton-Raphson iteration loop.
factory.setMode(YBus); gridpack::mapper::FullMatrixMap<PFNetwork> mMap(network); boost::shared_ptr<gridpack::math::Matrix> Y = mMap.mapToMatrix();
factory.setSBus(); factory.setMode(RHS); gridpack::mapper::BusVectorMap<PFNetwork> vMap(network); boost::shared_ptr<gridpack::math::Vector> PQ = vMap.mapToVector();
factory.setMode(Jacobian); gridpack::mapper::FullMatrixMap<PFNetwork> jMap(network); boost::shared_ptr<gridpack::math::Matrix> J = jMap.mapToMatrix(); boost::shared_ptr<gridpack::math::Vector> X(PQ->clone());
The first call sets the internal p_mode variable in all network components to “YBus”. The second call constructs a FullMatrixMap object mMap and the third line uses the mapToMatrix method to generate a Y-matrix based on the “YBus” mode. The factory then calls the setSBus method that sets some additional network component parameters (again, by looping over all buses and invoking a setSBus method on each bus). The next three lines set the mode to “RHS” create a BusVectorMap object and create the right hand side vector in the powerflow equations using the vectorToMap method. This builds the vector based on the “RHS” mode. The next three lines create the Jacobian using the same pattern as for the Y-matrix. The mode gets set to “Jacobian”, another FullMatrixMap object is created and this is used to create the Jacobian using the mapToMatrix method. Two separate mappers are used to create the Y-matrix and the Jacobian. This is required unless there is some reason to believe that the “YBus” and “Jacobian” modes generate matrices with the same dimensions and the same fill pattern. This is not generally the case, so different mappers should be created for each matrix in the problem. The last line creates a new vector by cloning the PQ vector. The X vector has the same dimension and data layout as PQ so it could be used with the vMap object.
Once the vectors and matrices for the problem have been created and set to their initial values it is possible to start the Newton-Raphson iterations. The code to set up the first Newton-Raphson iteration is
double tolerance = 1.0e-6; int max_iteration = 100; ComplexType tol;
gridpack::math::LinearSolver isolver(*J); isolver.configure(cursor);
int iter = 0;
X->zero(); isolver.solve(*PQ, *X); tol = X->norm2();
The first three lines define some parameters used in the Newton-Raphson loop. The tolerance and maximum number of iterations are hardwired in this example but could be made configurable via the input deck. The next line creates a linear solver based on the current value of the Jacobian, J. The call to the configure method allows values configuration parameters in the input file to be passed directly to the newly created solver. The iteration counter is set to zero and the value of X is also set to zero. The linear solver is called with PQ as the right hand side vector and X as the solution. An initial value of the tolerance is set by evaluating the norm of X. The calculation can now enter the Newton-Raphson iteration loop
while (real(tol) > tolerance && iter < max_iteration) {
vMap.mapToBus(X);
network->updateBuses();
factory.setMode(RHS); vMap.mapToVector(PQ); factory.setMode(Jacobian); jMap.mapToMatrix(J);
gridpack::math::LinearSolver solver(*J); solver.configure(cursor); X->zero(); solver.solve(*PQ, *X); tol = X->norm2(); iter++; }
This code starts by pushing the values of the solution vector back on to the buses using the same mapper that was used to create PQ. The network then calls the updateBus routine so that the ghost buses have the new values the parameters from the solution vector. New values of the Jacobian and right hand side vector are created based on the solution values from the previous iteration. Note that since J and PQ already exist, the mappers are just overwriting the old values instead of creating new data objects. The new Jacobian matrix is used to create a new linear solver and then to get a new set of values for the solution vector X. If the norm of this vector is still larger than the tolerance, the loop goes through another iteration or until the number of iterations reaches the value of max_iteration.
If the Newton-Raphson loop converges, then the calculation is essentially done. The last part of the calculation is to write out the results. This can be accomplished using the code
gridpack::serial_io::SerialBusIO<PFNetwork> busIO(128,network);
busIO.header("\n Bus Voltages and Phase Angles\n");
busIO.header("\n Bus Number Phase Angle");
busIO.header(" Voltage Magnitude\n");
busIO.write();
The first line creates a serial bus IO object that assumes that no line of output will exceed more than 128 characters. The next three lines write out the header for the output data and the last line writes a listing of data from all buses. This completes the execute method and the overview of the powerflow application.